Juros Compostos

O Poder dos juros compostos

Se você for uma pessoa disciplinada que consegue poupar uma certa quantia por mês, terá tranquilamente, após os 60 anos, 1 milhão na conta. Mas é necessário começar a poupar cedo.

É importante deixar claro que para isso acontecer, você deve procurar uma aplicação que ofereça uma rentabilidade considerável. Não é difícil encontrar boas aplicações no mercado para este tipo de aplicação. Um tipo de aplicação conservadora no Brasil é a renda fixa, como o CDB, por exemplo.

Renda fixa é garantida pelo Fundo Garantidor de Crédito (FGC) contra falências de bancos ou qualquer instituição que ofereça este tipo de aplicação, para aplicações até 250 mil reais. Isto é, caso a instituição venha a falir, o fundo o reembolsa até o o limite de 250 mil reais por CPF/CNPJ.

A família de renda fixa é grande, os mais conhecidos são: LCI (Letra de Crédito de Imobiliário), LCA (Letra de Crédito do Agronegócio), CDB (Certificado de Depósito Bancário), LC (Letra de Câmbio) e Tesouro Direto.

Quanto poupar por mês?

É importante ter disciplina para atingir um objetivo. Independente da profissão que você tenha, reserve 20% do seu salário para aplicar em renda fixa.

Com apenas 20% do seu salário já é um ponto de partida para atingir os seu objetivo. Essa porcentagem não é fixa, se no mês seguinte você conseguir colocar acima desse percentual, ótimo, pois com os juros compostos, quanto maior o saldo, maior será o rendimento.

Caso você aplique um valor inicial de R$ 1.000,00 e fizesse um aporte mensal de R$ 900,00, com uma taxa de juros anual de 6%, em 30 anos você chegaria a 1 milhão de reais. Veja na tabela abaixo:

Mês	Aportes	Juros Mensal	Juros Total	Acumulado
0	1.000,00	0	0	1.000,00
1	1.900,00	4,89	4,88	1.904,89
2	2.800,00	9,33	14,22	2.814,22
3	3.700,00	13,78	28,00	3.728,00
4	4.600,00	18,26	46,26	4.646,26
5	5.500,00	22,76	69,02	5.569,02
6	6.400,00	27,28	96,30	6.496,30
7	7.300,00	31,83	128,13	7.428,13
8	8.200,00	36,39	164,52	8.364,52
9	9.100,00	40,98	205,50	9.305,50
10	10.000,00	45,59	251,09	10.251,09
—	—	—	—	—
378	341.200,00	4.813,61	646.884,04	988.084,04
379	342.100,00	4.841,61	651.725,65	993.825,65
380	343.000,00	4.869,74	656.595,39	999.595,39

O gráfico abaixo mostra os dados da tabela ao longo do tempo. Perceba que os juros (em verde) começa a ter um crescimento ascendente e, após o 300º mês, o total em juros ultrapassa o aporte mensal (em azul).

Dessa forma, o valor acumulado (em vermelho) já contém uma parcela muito significante de juros do que do aporte mensal.

Diferença entre Juros Simples e Compostos

Podemos elencar algumas características básicas entre os juros simples e compostos:

Juros Simples

• Os juros simples rendem mensalmente ou anualmente sobre o valor inicial aplicado;
• Os rendimentos em juros simples são iguais, sem alteração a longo prazo;
• Tem crescimento linear, como uma reta;

Juros Compostos

• Os juros compostos rendem somente no vencimento da aplicação;
• Os rendimentos por juros compostos tem crescimento ascendente, isto é, a cada mês os juros são calculados em cima do capital mais os rendimentos anteriores; isto faz com que os juros do mês seguinte sejam maiores que o do mês anterior.
• Tem crescimento exponencial, cresce muito mais rápido, formando uma curva ascendente.

Para entender melhor veja com fica o montante da aplicação mês a mês com juros compostos:

Primeiro mês:

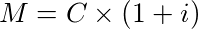
Segundo mês:

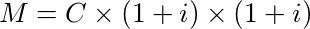
Terceiro mês:

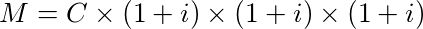
Quarto mês:

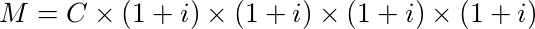
Quinto mês

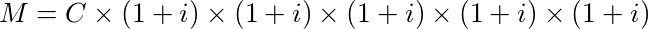
E assim por diante. Para cada mês os juros são calculados em cima do capital inicial C, mais os juros mês a mês. Esse tipo de remuneração em juros compostos com o passar do tempo tende a ser muito rentável. Pois tem um crescimento exponencial.

Fórmula para calcular o Montante em juros compostos

Para simplificar, obtemos a fórmula a seguir que representa o montante, ou seja, o valor final com o capital mais os juros aplicados:

Onde:

• M é o montante final obtido na aplicação, ou seja, o saldo após a aplicação do juros;
• i é a taxa de juros aplicada, em porcentagem;
• C é o capital ou valor inicial aplicado;
• t é o tempo total da aplicação.

A taxa de juros i deve ser escrita na forma decimal. Para transformar um número em decimal, divida ele por 100, pois a taxa é em porcentagem.

Fórmula para calcular juros compostos

O cálculo somente dos juros, ou seja, o rendimento que a aplicação obteve, é obtido pela seguinte fórmula:

Onde:

• J são os juros;
• M é o montante que pode ser calculado pela fórmula do montante acima;
• C é o capital ou valor inicial aplicado.

Importante:

Quando aplicarmos esta fórmula devemos ficar atentos as seguintes regras:

• Se a taxa i for ao ano, o tempo t deve ser reduzido à unidade de ano;
• Caso a taxa i for ao mês, o tempo t deve ser reduzido a unidade de mês;
• Se a taxa i for ao dia, o tempo t deve ser reduzido a unidade de dia.

Exercícios resolvidos de juros compostos

Na aplicação de R$ 1.000,00 durante 5 meses, à taxa de juros de 2% a.m., temos, contada uma capitalização mensal, 5 períodos de capitalização, ou seja, a aplicação inicial vai render 5 vezes.

Observando o crescimento do capital a cada período de capitalização, temos:

1º período:

100% ⇒ R$ 1.000,00 (valor inicial aplicado, corresponde a 100%)

102% ⇒ M = R$ 1.020,00 (esta é a nova base de cálculo para o período seguinte, valor inicial (100%) mais a taxa de juros de 2% ao mês, ou seja, rendimento de 20 reais no primeiro mês)

Veja na tabela abaixo os rendimentos mês a mês:

	CAPITAL	MONTANTE
2º período:	R$ 1.020,00 × 1,02	= R$ 1.040,40
3º período:	R$ 1.040,40 × 1,02	= R$ 1.061,21
4º período:	R$ 1.061,21 × 1,02	= R$ 1.082,43
5º período:	R$ 1.082,43 × 1,02	= R$ 1.104,08

Atenção: o 1,02 vem da fórmula M = C x (1 + i): M = 1.000,00 x (1 + 0,02) = 1.000,00 x 1,02. Obtivemos esse 0,02 de 2% ou ²⁄₁₀₀ = 0,02.

Portanto, o montante ao final dos 5 meses será R$ 1.104,08.

No cálculo, tivemos:

• M = R$ 1.000 × 1,02 × 1,02 × 1,02 × 1,02 × 1,02
• M = R$ 1.000 × (1,02)⁵
• M = R$ 1.000 × 1,10408
• M = R$ 1.104,08

Este é o montante em um período de 5 meses.

Generalizando, o cálculo  do montante a juros compostos será dado pela expressão abaixo:

onde:

• M é o montante final;
• i é a taxa de juros aplicada;
• C é o capital ou valor inicial.

Foi o que fizemos acima no cálculo dos rendimentos em cada período.

Para calcular os juros total basta diminuir o montante principal pelo capital aplicado.

J  =  R$1.104,08  –  R$1.000,00$$ = R$104,08

Assim, depois de 5 meses deverá ser pago R$104,08 de juros.

(UFMT) Uma financiadora oferece empréstimo por um período de 4 meses, sob as seguintes condições:

• I) Taxa de 11,4% ao mês, a juros simples;
• II) Taxa de 10% ao mês, a juros compostos.

Uma pessoa fez um empréstimo de R$ 10.000,00 optando pela condição I. Em quantos reais os juros cobrados pela condição I serão menores do que os cobrados pela condição II?

Para calcular os juros da condição I, basta utilizarmos a fórmula de juros simples, logo: J = C.i.t = 10000 . 0,114 . 4 = 4560

Portanto, em juros simples, será cobrado R$ 4.560,00.

Para calcularmos os juros na condição II, devemos utilizar a fórmula para calcular o montante de juros compostos, assim: M = C(1 + i)^t = 10000(1 + 0,1)⁴ = 10000 . 1,1⁴ = 10000 . 1,4641 = 14641

Agora que já calculamos o montante, podemos retirar desse valor o total cobrado em juros. Para isso basta utilizarmos o fórmula: J = M – C = 14641 – 10000 = 4641

Para sabermos qual condição é melhor, devemos realizar a diferença entre os juros cobrados:

Condição II – Condição I = 4641 – 4560 = 81

Portanto, os juros cobrados na condição I, em juros simples, serão menores que na condição II, em juros compostos. A diferença é de R$ 81,00.