binomio de Newton

O Binômio de Newton refere-se a potência na forma (x + y)n , onde x e y são números reais e n é um número natural.

O desenvolvimento do binômio de Newton em alguns casos é bastante simples. Podendo ser feita multiplicando-se diretamente todos os termos.

Contudo, nem sempre é conveniente utilizar esse método, pois de acordo com o expoente, os cálculos ficarão extremamente trabalhosos.

Exemplo

Represente a forma expandida do binômio (4 + y)3:

Como o expoente do binômio é 3, vamos multiplicar os termos da seguinte forma:
(4 + y) . (4 + y) . (4 + y) = (16 + 8y + y2) . (4 + y) = 64 + 48y + 12y2 + y3

Fórmula do Binômio de Newton

O binômio de Newton é um método simples que permite determinar a enésima potência de um binômio.

Esse método foi desenvolvido pelo inglês Isaac Newton (1643-1727) e é aplicado em cálculos de probabilidades e estatísticas.

A fórmula do binômio de Newton podendo ser escrita como:

(x + y)n = Cn0 y0 xn + Cn1 y1 xn - 1+ Cn2 y2 xn - 2 +... + Cnn yn x0

ou

Sendo,

Cnp : número de combinações de n elementos tomados p a p.

n! : fatorial de n. É calculado como n = n (n - 1)(n - 2) . ... . 3 . 2 . 1

p! : fatorial de p

(n - p)! : fatorial de (n - p)

Exemplo

Efetuar o desenvolvimento de (x + y)5:

Primeiro escrevemos a fórmula do binômio de Newton

Agora, devemos calcular os números binomiais para encontrar o coeficiente de todos os termos.

Considera-se que 0! = 1

Assim, o desenvolvimento do binômio é dado por:

(x + y)5 = x5 + 5x4y + 10 x3y2 + 10x2y3 + 5xy4 + y5

Termo Geral do Binômio de Newton

O termo geral do binômio de Newton é dado por:

Exemplo

Qual é o 5º termo do desenvolvimento de (x + 2)5, de acordo com as potências decrescentes de x?

Como queremos T5 (5º termo), então 5 = k +1 ⇒ k = 4.

Substituindo os valores no temos geral, temos:

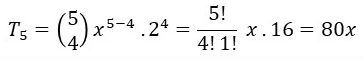
Binômio de Newton e Triângulo de Pascal

O triângulo de Pascal é um triângulo numérico infinito, formado por números binomiais.

O triângulo é construído colocando-se 1 nos lados. Os demais números são encontrados somando os dois números imediatamente acima deles.

Representação do triângulo de Pascal

Os coeficientes do desenvolvimento de um binômio de Newton podem ser definidos utilizando o triângulo de Pascal.

Desta maneira evita-se os cálculos repetitivos dos números binomiais.

Exemplo

Determine o desenvolvimento do binômio (x + 2)6.

Primeiro é necessário identificar qual linha iremos usar para o binômio dado.

A primeira linha corresponde ao binômio do tipo (x + y)0, desta forma, usaremos a 7ª linha do triângulo de Pascal para o binômio de expoente 6.

(x + 2)6 = 1x6 + 6x5.21 + 15x4.22 + 20x3.23 + 15x2.24 + 6x1.25 + 1x0.26

Assim, o desenvolvimento do binômio ficará:

(x + 2)6= x6 + 12x5 + 60x4 + 160x3 + 240x2 + 192x + 6